1. 서론
오늘은 최소공배수를 구하는 알고리즘 문제를 풀이하였다.
최소공배수를 구하려면 최대공약수를 구해야했고, 유클리드 호제법을 이용하였다.
2. 문제
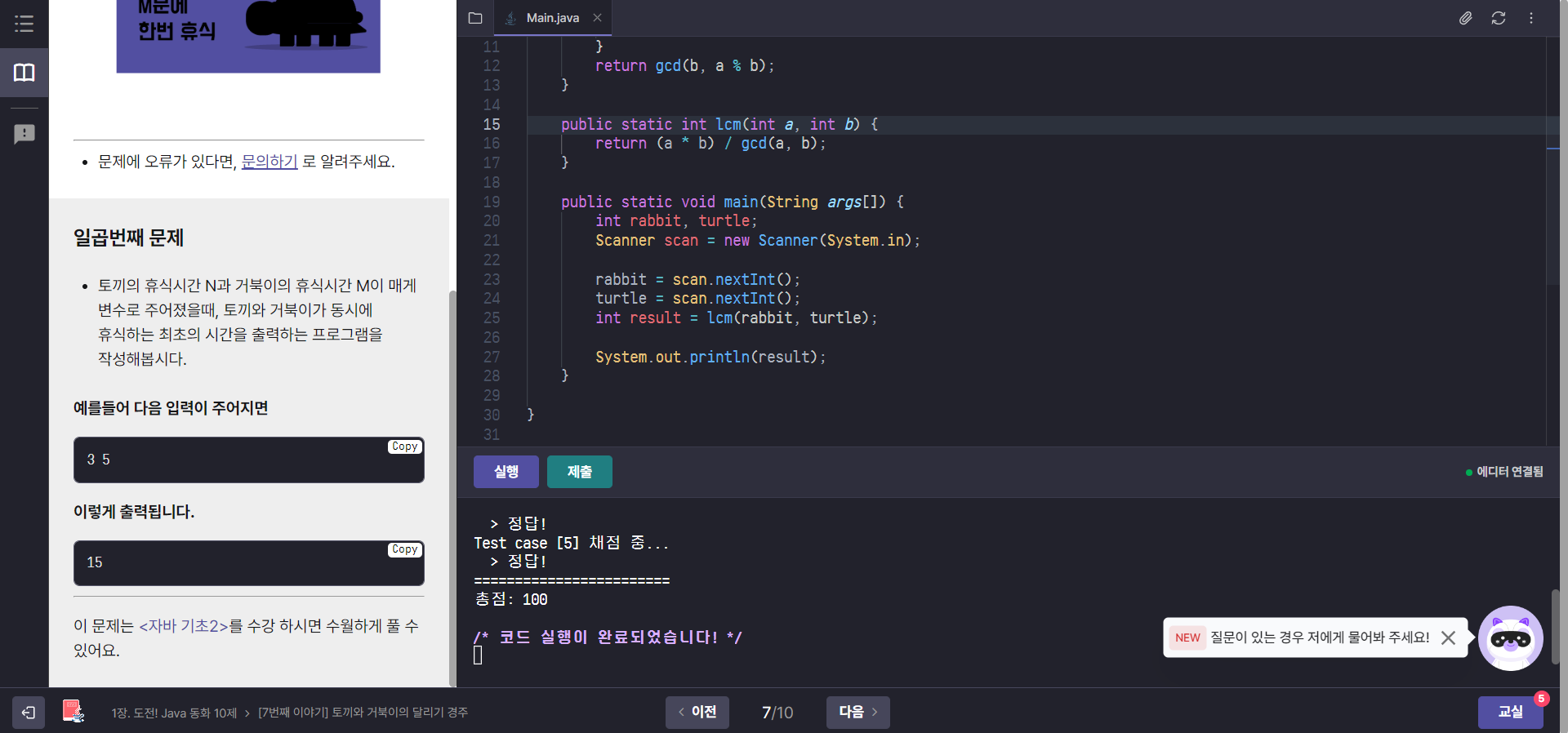
토끼와 거북이의 달리기 경주
토끼와 거북이가 달리기 경주를 시작했다.
토끼는 N분에 한번 휴식을 하고 거북이는 M분에 한번 휴식을 한다고 한다.
토끼와 거북이가 처음으로 같은 타이밍에 쉬는 시간은 언제일까?
토끼의 휴식시간 N과 거북이의 휴식시간 M이 매게 변수로 주어졌을때, 토끼와 거북이가 동시에 휴식하는 최초의 시간을 출력하는 프로그램을 작성하라.
문제 풀이
약간의 스토리가 가미되었지만 한 줄로 요약하면 입력받은 두 수의 최소공배수를 구하라는 문제이다.
여러가지 해결 방법이 있겠지만 본인은 유클리드 호제법을 이용하여 풀이를 진행하였다.
A와 B의 최대공약수(GCD)를 구하는데 A > B라면 A%B = r이라면 A와 B의 최대공약수는 B와 r의 최대공약수와 같다. 이를, 재귀함수로 계속 반복하여 나머지가 0이 되는 순간의 b가 최대공약수가 된다.
최소 공배수는 두 수의 곱에서 최대공약수를 나눈 값과 같다.
package elice;
import java.util.*;
public class Main {
public static int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
public static int lcm(int a, int b) {
return (a * b) / gcd(a, b);
}
public static void main(String args[]) {
int rabbit, turtle;
Scanner scan = new Scanner(System.in);
rabbit = scan.nextInt();
turtle = scan.nextInt();
int result = lcm(rabbit, turtle);
System.out.println(result);
}
}유클리드 호제법을 적용하는 경우 a > b 로 설정해야 올바른데, a가 더 큰 수여야 두 수를 나누었을 때의 나머지가 항상 양수로 유지되기 때문이다. 코드에 a > b를 직접적으로 넣지 않았지만 문제가 없다.
예를 들어, gcd(12, 18)을 호출하는 경우 a가 더 큰수가 아니지만 결국 gcd(b, a%b)를 호출하여 gcd(18, 12)로 다시 함수가 호출되기 때문이다.
'기타 > 엘카데미' 카테고리의 다른 글
| [엘카데미 챌린지] 10일차 Java 레벨 테스트 (5) (0) | 2023.07.26 |
|---|---|
| [엘카데미 챌린지] 9일차 Java 레벨 테스트 (4) (0) | 2023.07.25 |
| [엘카데미 챌린지] 7일차 Java 레벨 테스트 (2) (0) | 2023.07.23 |
| [엘카데미 챌린지] 6일차 Java 레벨 테스트 (1) (0) | 2023.07.22 |
| [엘카데미 챌린지] 5일차 SQL 레벨 테스트 마무리 (0) | 2023.07.21 |
